이번 포스팅은 CVML의 APEX 포스팅을 구경 중 FP16이 성능향상을 내는 방법이 궁금해서 찾아보며 적은 글이다.
NVIDIA APEX
GPU를 업그레이드 하지 않고 batch size를 늘릴 수 있는 방법이 있다. 바로 NVIDIA APEX를 사용하면 된다. NVIDIA에서 만든 "A Pytorch EXtension"라는 패키지로 크게 mixed precision training과 distributed training 기능이 있다.
NVIDIA/apex
A PyTorch Extension: Tools for easy mixed precision and distributed training in Pytorch - NVIDIA/apex
github.com
mixed precision training에 AMP(Automatic Mixed Precision)을 통해 코드 단 3줄로 정확도를 유지시키며 처리 속도를 높힐 수 있다고 한다.

우선 속도관점에서, 위 figure을 보면 기존 보다 2.3 배부터 4.9배 까지 속도 향상이 일어났다. 배치 사이즈에만 2배 증가하였다.
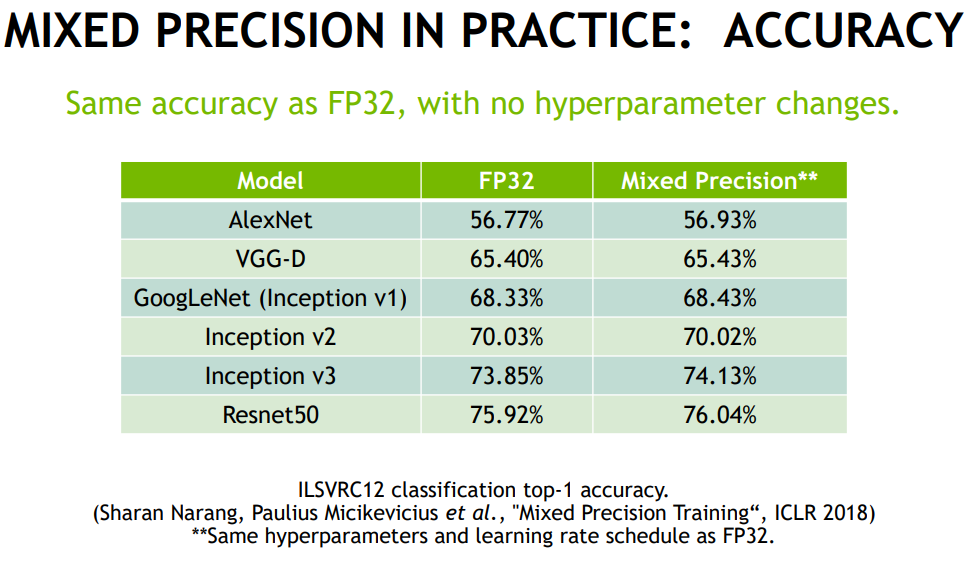
또한 성능에서도 비슷하거나 조금 향상된 결과를 얻을 수 있다.
Code
아래의 단 3줄 코드 만으로 위의 향상이 가능하다. (참고)
NVIDIA/apex
A PyTorch Extension: Tools for easy mixed precision and distributed training in Pytorch - NVIDIA/apex
github.com
# Added after model and optimizer construction
model, optimizer = amp.initialize(model, optimizer, flags...)
...
# loss.backward() changed to:
with amp.scale_loss(loss, optimizer) as scaled_loss:
scaled_loss.backward()위의 amp.initialize(model, optimizer, flags...) 중 flags에는 여러 최적화 기법 (OPT_LEVEL) 설정이 가능하다. NVIDIA APEX에 관한 소개 및 자세한 사용법은 CVML의 블로그를 참고하면 많은 정보를 얻을 수 있다.
[NVIDIA APEX] Amp에 대해 알아보자 (Automatic Mixed Precision)
version update 20-07-25 : amp 모듈이 pytorch 1.5.0 버전부터 기본 라이브러리에 추가되고 있음! pytorch 를 이용해 모델을 학습하다 보면 더 많은 batch size를 학습시키고 싶고 더 빠르게 학습시키고 싶은 생..
cvml.tistory.com
HOW??
그렇다면, 어떻게 속도 향상이 일어날 수 있을까? 이에 FP16(16 bit floating points) 사용이 핵심이다. Mixed Precision은 처리 속도를 높이기 위해 FP32와 FP16 연산을 섞어서 사용한다.
그렇다면 이 블로깅의 핵심인 FP16과 FP32 차이를 알기 전에 기본적인 FP(Floating Points)에 대해 알아보자.
Floating Points
컴퓨터는 기본적으로 2진수를 사용한다. 하지만 142.3 을 2진수로 표현해보면...?
142 -> 1000 1110
.3 -> 0.0100110011... # 무한 반복2진수로 표현하지 못하는 실수가 존재한다. 따라서 컴퓨터에는 근사 값이 저장된다. 이때 사용되는 방법이 있는데 고정 소수점과 부동 소수점이다.
고정 소수점은 정해진 bit를 쪼개서, 부호(1 bit), 정수(n bit), 소수(m bit)를 사용한다. 하지만 정수 표현 bit를 늘리면 소수 표현 bit가 적어지며 정밀한 숫자를 표현하기 힘들다. 마찬가지로 소수 표현 bit를 늘리면 큰 숫자를 표현할 수 없다. 이에 부동 소수점을 통해 이 문제를 해결할 수 있다.
부동 소수점은 부호(1 bit), 지수(e bit), 소수(f bit)를 사용한다.

아래 예제는 십진수 12.31을 IEEE754 표준 부동 소수점으로 표현하는 예시이다.
1. [이진수 변환] 1100.010011...
2. [정규화] 1.100010011... × 2^3
3. 지수부: 3, 가수부: 100010011...
4. [지수부 + 바이어스*] 3 + 127 = 130 -> 1000 0010
따라서 십진수 12.31은 IEEE754 기준에 의해 0 1000 0010 100 0100 1111 0101 1100 0011 로 표현이 된다.
*바이어스: 지수부분(8bit)이 표현 가능 숫자는 -127 ~ 128 이지만 부호부가 존재하지 않기 때문에 0000 0000 을 -127로, 1111 1111을 128로 정의
FP16 vs FP32
부동소수점에 대해 알게 되었다면, 이제 FP16과 FP32 차이에 대해 알아보자. IEEE754 표준 부동 소수점에 의하면 FP32의 경우 8bits 지수부(magnitude)와 23bits 가수부(precision)가 존재한다. 하지만 대부분의 딥러닝의 경우 모든 자리의 지수부와 가수부가 필요한 경우가 거의 없다. NVIDIA는 대부분의 weight와 gradient는 16bits로만 표현이 가능할 수 있으며, 그렇지 않은 gradient의 경우(매우 작은 gradient), 단순히 scaling up으로 이를 해결 할 수 있다고 분석했다. 따라서 FP16을 사용하여 5bits 지수부, 10bits 가수부로 줄일 수 있다 고 한다. 즉 정확도는 유지하면서 계산 효율성을 가지게된다.
하지만 당연히 underflow와 overflow의 risk는 존재한다. (underflow -> 학습x, overflow -> 잘못된 학습) 이를 weight과 gradient의 크기와 방향만을 중요한 요인으로 가정한 후, precision을 줄임으로써 해결하는 방안도 제시되고 있다(horovod의 bfloat16).
horovod/horovod
Distributed training framework for TensorFlow, Keras, PyTorch, and Apache MXNet. - horovod/horovod
github.com
이러한 까닭으로 FP16만 사용하면 최대 25배 까지 계산 가속이 되며, 필요한 메모리를 줄일 수 있게 된다. 또한 정확한 계산이 필요한 경우 위에서 언급한 옵션을 이용하여 정확한 계산이 필요한 부분은 FP32로 나머지 연산은 FP16 을 이용할 수 있다.
References
Computer Vision :)
cvml.tistory.com
Pytorch Nvidia Apex를 이용한 모델 학습 최적화
Language Model Pretraining을 Colab에서 하다 보면, 학습시간도 단축하고 싶고, 배치 사이즈도 늘려서 학습하고 싶다는 생각이 들게 됩니다.자료를 찾아보다가 위와 같은 문제를 단 몇줄의 코드로 해결
velog.io
What is the difference between FP16 and FP32 when doing deep learning?
Answer (1 of 3): This is a well-timed question, as we just added FP16 support to Horovod last Friday. So naturally, I’m itching to talk more about it! The value proposition when using FP16 for training a deep neural network is significantly faster traini
www.quora.com
'MLOps' 카테고리의 다른 글
| TorchScript? torch.jit.script 에러 유형 및 해결 방법 (0) | 2021.05.01 |
|---|---|
| [PyTorch] .detach().cpu().numpy()와 .cpu().data.numpy() ? (0) | 2021.04.28 |
| Kubeflow - Pipelines 소개 - 2 (0) | 2021.02.24 |
| Kubeflow - Pipelines 소개 - 1 (0) | 2021.02.24 |
| [Toy] Trigger using Slack (0) | 2021.02.01 |



